题目连接：https://www.nowcoder.com/practice/8a19cbe657394eeaac2f6ea9b0f6fcf6

题目大意：给定二叉树的先序遍历和中序遍历结果，建立这棵二叉树。输入保证二叉树无重复结点。

 

思路

首先回顾一下先序遍历和中序遍历。

先序遍历是先访问左子树，再访问当前结点，最后访问右子树。

中序遍历是先访问左子树，再访问右子树，最后访问当前结点。

由于题目保证要建立的二叉树不存在重复结点，我们就可以利用先序遍历和中序遍历的特点来建立二叉树。

 

以先序{1, 2, 4, 7, 3, 5, 6, 8}和中序{4, 7, 2, 1, 5, 3, 8, 6}为例，显然整棵树的根结点一定是先序遍历的第一个，即1。

在中序序列中把1找到，1左边的4,7,2就是左子树，1右边的5,3,8,6就是右子树。

再来观察左子树{2,4,7}/{4,7,2}，同样先序序列的第一个结点即为左子树的根结点，即2。

在中序序列中找到2，2左边的{4,7}就是它的左子树，2已经是中序序列的最后一个，它没有右子树。

再来看{4,7}/{4,7}这棵子树，这棵子树只有两个结点，并且先序和中序遍历的顺序是一样的，显然4是根结点，7是右子树的叶结点。反之，假如为{4,7}/{7,4}，则4为根结点，7为左叶结点。

至此已经得到了整棵树的左半边：

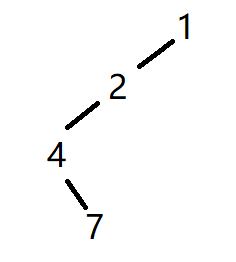
回头看1的右子树{3,5,6,8}/{5,3,8,6}，显然在这棵子树中3是根结点，{5}/{5}是它的左子树，{6,8}/{8,6}是它的右子树。

在左子树{5}/{5}中只有一个结点。

在右子树{6,8}/{8,6}中，显然先序遍历和中序变量的顺序不一样，易知6是根结点，8是右叶结点。

现在整棵树都得到了：

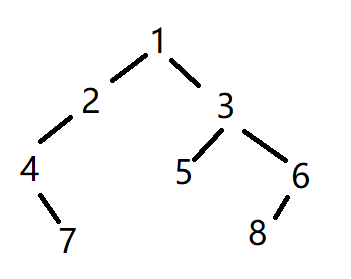
不难发现上面这个分析过程是递归分治的，根据这个思路就可以写出递归题解。

 

代码

import java.util.LinkedList;import java.util.Queue;/** * @author yuan * @version 0.1 * @date 2019/6/4 */public class RebuildBinaryTree {    private class TreeNode {        int val;        TreeNode left;        TreeNode right;        TreeNode(int x) {            val = x;        }    }    private int[] preorder;    private int[] inorder;    /**     * 递归方法。根据先序和中序遍历序列构建子树。     *     * @param preorderStart 子树在先序遍历序列中的第一个结点所在下标     * @param inorderStart  子树在中序遍历序列中的第一个结点所在下标     * @param num           子树结点数目     * @return 子树根结点     */    private TreeNode reConstructBinaryTree(int preorderStart, int inorderStart, int num) {        TreeNode root = null;        if (inorderStart >= inorder.length || preorderStart < 0) {            return root;        }        if (num == 1) {            root = new TreeNode(preorder[preorderStart]);            return root;        } else if (num == 2) {            root = new TreeNode(preorder[preorderStart]);            // 先序和中序一样则应为根+右子结点，否则为根+左子结点            if (preorder[preorderStart] == inorder[inorderStart]) {                root.right = new TreeNode(preorder[preorderStart + 1]);            } else {                root.left = new TreeNode(preorder[preorderStart + 1]);            }            return root;        }        TreeNode left = null;        TreeNode right = null;        // 根结点必为先序第一个，据此查找根结点在中序中的位置        for (int i = inorderStart; i < inorderStart + num; i++) {            if (inorder[i] == preorder[preorderStart]) {                // i大于inorderStart说明左子树存在，左子树先序从preorderStart+1开始，左子树中序从inorderStart开始，左子树结点数目为i-inorderStart                if (i > inorderStart) {                    left = reConstructBinaryTree(preorderStart + 1, inorderStart, i - inorderStart);                }                // i小于inorderStart+num-1说明右子树存在，右子树先序从preorderStart+(i-inorderStart)+1开始，右子树中序从i+1开始，右子树结点数目为num-(i-inorderStart)-1                if (i < inorderStart + num - 1) {                    right = reConstructBinaryTree(preorderStart + i - inorderStart + 1, i + 1, num - i + inorderStart - 1);                }                root = new TreeNode(preorder[preorderStart]);                root.left = left;                root.right = right;                break;            }        }        return root;    }    public TreeNode reConstructBinaryTree(int[] preorder, int[] inorder) {        this.preorder = preorder;        this.inorder = inorder;        return reConstructBinaryTree(0, 0, preorder.length);    }    /**     * 测试用，BFS打印     *     * @param root 根结点     */    public void printTree(TreeNode root) {        Queue
     
       queue = new LinkedList<>();        queue.offer(root);        StringBuilder result = new StringBuilder();        result.append(root.val);        while (!queue.isEmpty()) {            TreeNode node = queue.poll();            if (node.left == null && node.right == null) {                continue;            }            if (node.left != null) {                queue.offer(node.left);                result.append(",").append(node.left.val);            } else {                result.append(",#");            }            if (node.right != null) {                queue.offer(node.right);                result.append(",").append(node.right.val);            } else {                result.append(",#");            }        }        System.out.println(result.toString());    }    public static void main(String[] args) {//        int[] preorder = {1, 2, 3, 4, 5, 6, 7};//        int[] inorder = {3, 2, 4, 1, 6, 5, 7};//        int[] preorder = {1, 2, 4, 3, 5, 6};//        int[] inorder = {4, 2, 1, 5, 3, 6};        int[] preorder = {1, 2, 4, 7, 3, 5, 6, 8};        int[] inorder = {4, 7, 2, 1, 5, 3, 8, 6};        RebuildBinaryTree solution = new RebuildBinaryTree();        solution.printTree(solution.reConstructBinaryTree(preorder, inorder));    }}
     

 

 附牛客网评论区最高赞代码，写法更加简洁

public TreeNode reConstructBinaryTree(int [] pre,int [] in) {    TreeNode root=reConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);    return root;}private TreeNode reConstructBinaryTree(int [] pre,int startPre,int endPre,int [] in,int startIn,int endIn) {    if(startPre>endPre||startIn>endIn)        return null;    TreeNode root=new TreeNode(pre[startPre]);    for(int i=startIn;i<=endIn;i++)        if(in[i]==pre[startPre]){            root.left=reConstructBinaryTree(pre,startPre+1,startPre+i-startIn,in,startIn,i-1);            root.right=reConstructBinaryTree(pre,i-startIn+startPre+1,endPre,in,i+1,endIn);            break;        }    return root;}